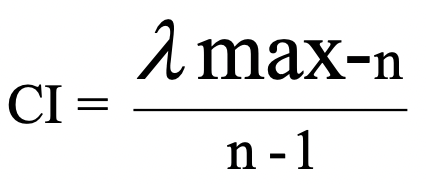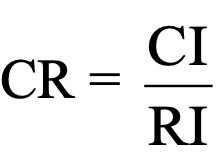disclaimer: artikel ini merupakan bagian kedua dari topik pairwise comparison, sebelum membaca artikel ini, diharapkan Anda membaca bagian pertama dengan judul: Pairwise Comparison in General

Pada artikel sebelumnya, kita sudah membahas mengenai pengertian dan manfaat pairwise comparison serta langkah-langkah dalam melakukan Analytical Hierarchy Process. Pada artikel ini, kita akan membahas bagaimana menyusun pairwise comparison matrix  yang dapat membantu dalam memberi peringkat, memprioritaskan, dan umumnya membandingkan barang.

Dalam menyusun prioritas dapat menggunakan skala Saaty (Zhang, Liu, & Yang, 2009), untuk berbagai persoalan, skala 1 sampai 9 adalah skala terbaik dalam mengekspresikan pendapat. Masing-masing perbandingan berpasangan dievaluasi dalam Saaty’sscale  1  – 9sebagai berikut;

Nilai dan definisi pendapat kualitatif dari skala perbandingan Saaty dapat dilihat pada tabel berikut ini:

1. Pengertian nilai tengah-tengah adalah jika elemen A sedikit lebih penting dari  elemen B  maka  kita  seharusnya  memberikan  nilai  3, namun jika nilai 3 tersebut dianggap masih terlalu besar dan nilai 1 masih  terlalu  kecil  maka  nilai  2  yang  harus  kita  berikan  untuk prioritas antara elemen A dengan elemen B.
2. Tabel diatas tidak disebutkan konversi nilai elemen A kurang penting dari elemen B karena pernyataan elemen A kurang penting dari elemen B sama dengan  pernyataan  nilai  elemen    B  lebih penting dari elemen A

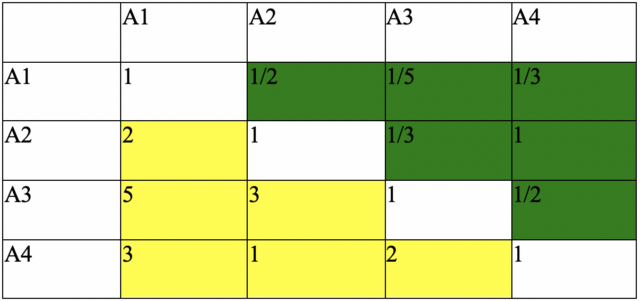
Perbandingan  dilakukan berdasarkan kebijakan pembuat keputusan  dengan  menilai  tingkat  kepentingan  satu  elemen  terhadap elemen  lainnya  Proses  perbandingan  berpasangan,  dimulai  dari  level hirarki  paling  atas  yang  ditujukan  untuk memilih  kriteria,  misalnya  A, kemudian  diambil  elemen  yang  akan  dibandingkan,  misal  A1,  A2,  A3 dan  A4.  Maka  susunan  elemen-elemen  yang  dibandingkan  tersebut  akan tampak seperti pada gambar matriks di bawah ini:

Cara mengisinya adalah dengan menganalisa prioritas antara elemen baris dibandingkan dengan elemen kolom. Dalam prakteknya kita hanya  perlu  menganalisa  prioritas  elemen yang  terdapat  dibawah  pada garis diagonal (kotak dengan warna dasar putih) yang ditunjukan dengan warna  kuning  atau  diatas  garis  diagonal  yang  ditunjukan  dengan  kotak warna hijau.

Apabila suatu elemen  dibandingkan  dengan  dirinya  sendiri  maka diberi nilai 1. Jika elemen i dibandingkan dengan elemen j mendapatkan nilai tertentu, maka elemen j  dibandingkan  dengan  elemen  i  merupakan kebalikannya.

Hal ini  sesuai  dengan  persamaan  matematika  yang  menyebutkan jika A:B= X, maka B : A = 1/X. Contoh: jika prioritas elemen A2 (baris) : elemen A1 (kolom)  =  2,  maka  prioritas  elemen  A1 (baris)  :  elemen  A2 (kolom)  =  1/2  (lihat  rumus   persamaan  perbandingan  matematika diatas).

Selanjutnya  adalah  menentukan  bobot  pada  tiap  elemen,  nilai bobot ini berkisar antara 0 – 1. dan total bobot untuk setiap kolom adalah

1. Cara menghitung bobot adalah angka pada setiap kotak dibagi denganpenjumlahan semua angka dalam kolom yang sama.Contoh : bobot dari  (elemen  A1,  elemen  A1)  =  1/  (1+2+5+3) = 0.090,  (elemen  A2,  elemen  A1)  =  2  /  (1+2+5+3)  =  181.
2. Penentuan nilai bobot prioritas. Caranya adalah dengan melakukan penjumlahan  setiap  nilai  bobot  prioritas  pada  setiap  baris tabel  dibagi  dengan  jumlah  elemen
3. Pengujian Konsistensi Logis

Penghitungan   konsistensi   logis   dilakukan   dengan   mengikuti langkah-langkah sebagai berikut :

• Mengalikan matriks awal dengan nilai bobot proritas bersesuaian.
• Menjumlahkan hasil perkalian per baris.
• Hasil penjumlahan    tiap    baris    dibagi    nilai    bobot    prioritasbersangkutan dan hasilnya dijumlahkan.
• Hasil c dibagi jumlah elemen, akan didapat λmaks.
• Indeks Konsistensi (CI) =

• Rasio Konsistensi =

dimana RI adalah Indeks Random konsistensi, dilihat dari table Random Indeks dibawah sesuai dengan ukuran n. Jika rasio konsistensi ≤ 0.1, hasil perhitungan data dapat dibenarkan/konsisten

Bibliography

Baxter, R. (2015, March 23). Use Pairwise Comparison to Prioritize Multiple Options. Retrieved from linkedin: https://www.linkedin.com/pulse/generating-value-using-pairwise-comparison-rod-baxter/

Ramík, J. (2020). Pairwise Comparisons Method: Theory and Applications in Decision Making. Switzerland: Springer Nature.

Zhang, Z., Liu, X., & Yang, S. (2009). A Note on the 1-9 Scale and Index Scale In AHP. Cutting-Edge Research Topics on Multiple Criteria Decision Making (pp. 630-634). Berlin, Heidelberg: Springer.